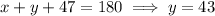Question

Please help! Asap. Parent in need of explanation of math problem?

Answer 1

The drawing shows that angles BAD and CAD are congruent, which means that the line segment AD bisects the angle BAC. By the angle bisector theorem,

`(CD)/(BD)=(AC)/(AB)`

But AB and AC are also shown to be congruent, so the right hand side reduces to 1, and we have
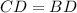`CD=BD`, which means CD and BD are also congruent.

AD is congruent to itself and happens to be a part of two triangles, ABD and ACD.

So by the side-side-side postulate, the triangles ABD and ACD are congruent, which means corresponding parts (sides and angles) are congruent to each other. And because triangles ABD and ACD are congruent, the "total" triangle ABC is isosceles, and AD must be perpendicular to BC. This last observation means that
`x=90`.

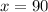In any triangle, the interior angles must sum to 180 degrees, so we have

`x+y+47=180\implies y=43`