Question

I can't figure this question out. 50 points if you can answer this for me!

Answer 1

(a)
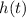`h(t)` gives the height at time
`t`, so the flare's starting height is given by
`h(0)`:

`h(0)=-5(0)^2+90(0)+1=1\,\mathrm m`

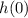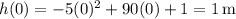
(b) There are several ways to find the maximum height of the flare. One is to complete the square and write
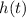`h(t)` in vertex form:

`-5t^2+90t+1=-5(t^2+18t)+1=-5(t^2-18t+81-81)+1=-5(t-9)^2+406`

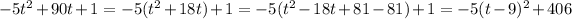
That is,
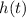`h(t)` describes a parabola whose vertex is located at (9, 406); the coefficient of -5 tells us that the parabola is concave, which means the parabola "opens" downward, and the vertex is a maximum. So the maximum height is 406 m.

(C) The flare hits the ground when
`h(t)=0`:

`-5t^2+90t+1=0\implies t=9\pm\sqrt{\frac{406}5}`

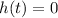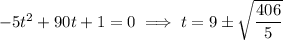
or at about
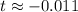`t\approx-0.011` and
`t\approx18.01`. We ignore the negative solution (negative time makes no physical sense).