Question

The graph of g(x) is shown below:

1) Write the equation of the line for its asymptote.

2) The function g(x) is a transformation of the parent function f(x)=13x. Describe the transformation that occurred using complete sentences.

Answer 1

Explanation:

1. asymptote is a line which the graph gets close but not touch. from the plot, it is y=2

2. f(x)=(1/3)^x so at x=0, f(0)=1 and x=-1, f(-1)=3

now g(0)=-1 and g(-1)=1

notice f(0)-g(0)=2` and (f(-1)-g(-1)=2

so g(x)=f(x)-2

transformation is that f(x) is moved down by 2 in the y-dir'n

Answer 2

1)

Horizontal asymptote states that the graph of a function approaches but never touches.

Therefore, the equation of the line for its asymptote is, y = -2.

2)

here, parent function
`f(x) = ((1)/(3))^x`.

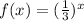Vertical shifts: To translate the function f(x) vertically, you can use the function g(x) = f(x) + k

if:

• k > 0, the graph of f(x) translated k units up.

• k < 0 , the graph of f(x) translated k units down.

As you can see in the graph as shown below the parent function is translated 2 units down to get g(x).

i.e,

`g(x) =((1)/(3))^x - 2`.

Therefore, the function
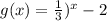`g(x) = (1)/(3))^x - 2` is the transformation of the parent functionf(x).