Answer:
Option 2 - E=7.5h
Explanation:
Given: The graph represents the direct variation function between earnings in dollars and hours worked.
To find : Which equation can be used to describe the direct variation function between E, the total earnings in dollars, and h, the number of hours worked?
Solution :
First we examine the graph,
The graph shows the linear equation.
The points (0,0) and (4,30) lie on the graph of the direct variation function.
We can use these points to determine the constant of proportionality which is the slope,
Formula to find slope is

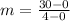
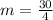

The total earnings E, varies directly proportional to the number of hours worked h.
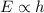
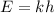
where k is the constant of proportionality.
k=7.5
Substitute, in E
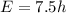
Therefore, Option 2 is correct.