Question

(HELP NEEDED ASAP!!!)The sequence below represents Marisa’s fine at the library for each day that she has an overdue book: $0.50, $0.65, $0.80, $0.95, $1.10, ... Which equation represents Marisa’s library fine as a function of a book that is n days overdue? f(n) = 0.15n f(n) = 0.50n f(n) = 0.15n + 0.35 f(n) = 0.50n + 0.15

Answer 1

C.
`f(n)=0.15n+0.35`

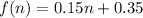
Step-by-step explanation:

We have been given a sequence representing the Marisa's fine at the library for each day that she has an overdue book: $0.50, $0.65, $0.80, $0.95, $1.10, ...

An arithmetic sequence is in form
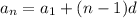`a_n=a_1+(n-1)d`, where
`a_n`= nth term of sequence.

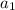`a_1`= 1st term of the sequence.

d= Common difference.

We can see from our sequence that 1st term of our sequence is 0.50.

Let us find common difference by subtracting 0.50 from 0.65.

`\text{Common difference}=0.65-0.50=0.15`

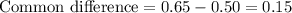
Upon substituting our values in arithmetic sequence we will get,

`f(n)=0.50+(n-1)0.15`

Upon distributing 0.15 we will get,

`f(n)=0.50+0.15n-0.15`

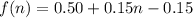
Now let us combine like terms.

`f(n)=0.15n+0.50-0.15`

`f(n)=0.15n+0.35`

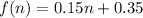
Therefore, the equation
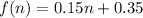`f(n)=0.15n+0.35` will represent Marisa’s library fine as a function of a book that is n days overdue and option C is the correct choice.