Question

Consider the function below. f(x) = 6x tan x, −π/2 < x < π/2 (a) find the vertical asymptote(s). (enter your answers as a comma-separated list. if an answer does not exist, enter dne.)

Answer 1

Answer: Does not exist.

Explanation:

Since, given function, f(x) = 6x tan x, where −π/2 < x < π/2.

⇒ f(x) =
`(6x sin x)/(cosx)`

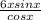
And, for vertical asymptote, cosx= 0

⇒ x = π/2 + nπ where n is any integer.

But, for any n x is does not exist in the interval ( -π/2, π/2)

Therefore, vertical asymptote of f(x) where −π/2 < x < π/2 does not exist.

Answer 2

x = −π/2, x = π/2

Explanation:

Given f(x) = 6x tan x and the interval −π/2 < x < π/2, we know that tan x has asymptotes in both extremes of the interval. To find the vertical asymptotes we evaluate the limit in the x-values we think asymptote can appear, in this case for x = −π/2 and x = π/2.

`\lim_(x \to\ (-\pi/2)-) 6x * tan x=`

`=\lim_(x\to\ (-\pi/2)-) 6x * \lim_(x\to\ (-\pi/2)-)tan x=`

`=-3 \pi * -\infty =\infty`

`\lim_(x\to\ (\pi/2)+) 6x * tan x=`

`=\lim_(x\to\ (\pi/2)+) 6x * \lim_(x\to\ (\pi/2)+)tan x=`

`=3 \pi * \infty =\infty`

Then, x = −π/2 and x = π/2 are vertical asymptotes.