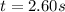Question

A juggler tosses a ball into the air . The balls height, h and time t seconds can be represented by the equation h(t)= -16t^2+40t+4 . Suppose the juggler missed and ball hit the ground . Find the maximum height of the ball and time it took to reach the ground. Round all answers to the nearest hundredth .

Answer 1

PART A

The given equation is


`h(t) = - 16 {t}^(2) + 40t + 4`

In order to find the maximum height, we write the function in the vertex form.

We factor -16 out of the first two terms to get,


`h(t) = - 16 ({t}^(2) - (5)/(2) t) + 4`

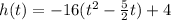
We add and subtract


`- 16(- (5)/(4) )^(2)`

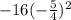
to get,


`h(t) = - 16 ({t}^(2) - (5)/(2) t) + - 16( - (5)/(4))^(2) - -16( - (5)/(4))^(2) + 4`

We again factor -16 out of the first two terms to get,


`h(t) = - 16 ({t}^(2) - (5)/(2) t + ( - (5)/(4))^(2) ) - -16( - (5)/(4))^(2) + 4`

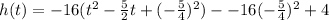
This implies that,


`h(t) = - 16 ({t}^(2) - (5)/(2) t + ( - (5)/(4)) ^(2) ) + 16( (25)/(16)) + 4`

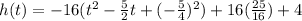
The quadratic trinomial above is a perfect square.


`h(t) = - 16 ( t- (5)/(4)) ^(2) +25+ 4`

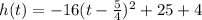
This finally simplifies to,


`h(t) = - 16 ( t- (5)/(4)) ^(2) +29`

The vertex of this function is


`V( (5)/(4) ,29)`

The y-value of the vertex is the maximum value.

Therefore the maximum value is,


`29`

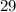
PART B

When the ball hits the ground,


`h(t) = 0`

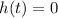
This implies that,


`- 16 ( t- (5)/(4)) ^(2) +29 = 0`

We add -29 to both sides to get,


`- 16 ( t- (5)/(4)) ^(2) = - 29`

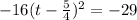
This implies that,


`( t- (5)/(4)) ^(2) = (29)/(16)`


`t- (5)/(4) = \pm \sqrt{ (29)/(16) }`


`t = (5)/(4) \pm ( √(29) )/(4)`


`t = ( 5 + √(29) )/(4) = 2.60`

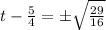
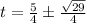
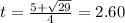
or


`t = ( 5 - √(29) )/(4) = - 0.10`

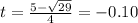
Since time cannot be negative, we discard the negative value and pick,


`t = 2.60s`