Question

Tickets to a school play cost $2 if bought in advance, and $3 if bought at the door. By selling all 400 of their tickets, $1030 was collected. Let x represent the number of tickets sold at the door. in terms of x how many of the tickets were sold in advance?

Answer 1

230 were sold at the door

170 were sold in advance

Explanation:

*i dont know if this is the proper way to do it but it has the correct answer

x=at door y=in advance

x+y=400

3x+2y=1030

y=-x+400

2y=-3x+1030

y=-3/2x+515

-x+400=-3/2x+515

x=230 y=170

Answer 2

230 tickets were sold at door and 170 tickets were sold in advance.

Explanation:

Let x represent the number of tickets sold at the door.

Let y be the tickets sold in advance.

Equations form as per given scenario are:

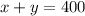`x+y=400` or x=400-y ......(1)

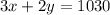`3x+2y=1030` ......(2)

Substituting the value of x from (1) in (2)

`3(400-y)+2y=1030`

=>
`1200-3y+2y=1030`

=>
`1200-1030=3y-2y`

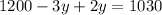
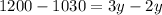
We get y = 170

And x =
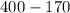`400-170` = 230

Hence, 230 tickets were sold at door and 170 tickets were sold in advance.