Question

Carrie wished to build a rectangular dog run along theside of her garage. The garage will serve as one side of the fence. If she has 180 ft of the fencing and wishes the fence to be 4times as long as it is wide,how many square ft will the fencing enclose?

Urgent please help a180 b1800 c3600

Answer 1

Given:

Carrie has 180 ft of the fencing and wishes the fence to be 4times as long as it is wide.

To Find:

The area in square feet that the fencing encloses.

Answer:

The fence encloses 3600 sq ft.

Explanation:

Let x denote the length of the dog run and y denote the width of the dog run.

Given that the garage wall serves as one side of the dog run, we are left with 3 other sides to instal the fence.

Carrie has 180ft of fencing with her, so the sum of the lengths of the 3 sides has to be equal to 180. We can represent this in the form of an equation as

`x+y+y=180\\\\x+2y=180\\\\x=180-2y`

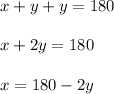
We are also given that Carrie wishes the fence to be 4 times as long as it is wide.

So,

`x=4y`

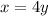
Replacing this value into the first equation, we have

`4y=180-2y\\\\ 6y=180\\\\ y=30`

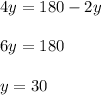
Therefore,

`x=(4)(30)=120`

Thus, the length of the dog run is 120ft and the width is 30ft.

The area enclosed will be equal to the length multiplied with the width. So,

`(120)(30)=3600`

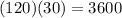
The fence encloses 3600 sq ft.