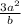Question

`((3a^2b)^3)/(9(ab)^4)`

Answer 1

You first multiply the outside exponents into the numbers in the parentheses.

When you have an exponent being multiplied directly to another exponent, you multiply the exponents together.

For example(because I am a bad explainer):

`(x^(2) )^4= x^(2(4)) = x^8`

`(x^4)^3 = x^(4(3)) = x^(12)`

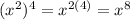
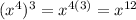
When you divide an exponent by an exponent, you subtract the exponents

For example:

`(x^4)/(x^1) =x^(4-1)=x^3`

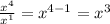
When you have a negative exponent, you move it to the other side of the fraction to make the exponent positive

For example:

`x^(-3)=(1)/(x^3)`

`(1)/(y^(-5))=(y^5)/(1)=y^5`

`((3a^2b)^3)/(9(ab)^4)`

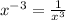
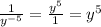
You can think of it like this if you want:

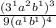`((3^1a^2b^1)^3)/(9(a^1b^1)^4)` Now multiply the outside exponents into the exponents in the parentheses

`(3^3a^6b^3)/(9(a^4b^4)) =(27a^6b^3)/(9(a^4b^4))` Divide 27 and 9

`(3a^6b^3)/(a^4b^4) =(3)(a^(6-4))(b^(3-4))=(3)(a^2)(b^(-1))=(3)(a^2)((1)/(b^1))=(3a^2)/(b)`

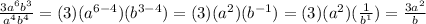
Your answer is
`(3a^2)/(b)`