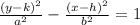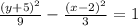Question

Write the equation of the hyperbola with center (2,-5), vertex (2,-2), and focus (2+-5+2sqrt3)

Answer 1

Its A for sure :)

Answer 2

option A :
`((y+5)^2)/(9) - ((x-2)^2)/(3)=1`

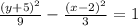
Explanation:

the equation of the hyperbola with center (2,-5), vertex (2,-2), and focus (2+-5+2sqrt3)

center is (2,-5), vertex is (2,-2). It is a vertical hyperbola

General equation for vertical hyperbola is

`((y-k)^2)/(a^2) - ((x-h)^2)/(b^2)=1`

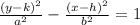
Center (2,-5) so h=2, k= -5

vertex is (2,-2)

We know vertex is (h, k+a), k=-5

k + a= -2

-5 + a = -2

so a = 3

Given focus (2+-5+2sqrt3)

Focus is (h , k+c), k= -5

`k+c= -5+2√(3)`

`-5+c= -5+2√(3)`

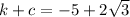
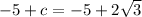
Add 5 on both sides

`c= 2√(3)`

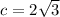
We need to find out b

c^2 = a^2 + b^2

`(2√(3))^2= 3^2 + b^2`

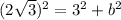
12 = 9 + b^2

b^2 = 3

we know a=3 so a^2 =9

we know h=2 and k = -5

Plug in all the values in general equation

`((y-k)^2)/(a^2) - ((x-h)^2)/(b^2)=1`

`((y+5)^2)/(9) - ((x-2)^2)/(3)=1`