Question

The following geometric sequences represent the population of two bacterial cultures at the 1 hour mark the 2 hour mark the 3 hour mark and so on culture A starts with more bacteria but culture b has a ratio of increase that is larger which culture will have the greater population at the 18 hour mark

Answer 1

Culture B

Explanation:

The explicit formula for a geometric sequence can be written as a function. First use the form

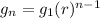`g_n=g_1(r)^(n-1)`, where g₁ is the first term and r is the common ratio.

For culture A, the common ratio is 900/600 = 1.5 and the first term is 600:

`g_n=600(1.5)^(n-1)`

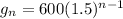
For culture B, the common ratio is 20/10 = 2 and the first term is 10:

`g_n=10(2)^(n-1)`

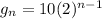
Next we write the explicit formula as a function. First we separate the exponent into two pieces. We can do this because the product property of exponents tells us when two powers with the same base are multiplied, we add them. This means we can separate them similarly.

For culture A,

`y=600(1.5)^n(1.5)^(-1)`

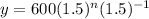
For culture B,

`y=10(2)^n(10)^(n-1)`

Next we evaluate the negative exponent. An exponent of -1 essentially "flips" the fraction.

For culture A, 1.5 = 3/2 and for culture B, 2 = 2/1:

Culture A:

`y=600(1.5)^n(2/3)`

Culture B:

`y=10(2)^n(1/2)`

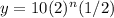
Lastly, we multiply the two numbers without exponents. For culture A,

`y=(600* 2/3)(1.5)^n\\\\y=(1200/3)(1.5)^n\\\\y=400(1.5)^n`

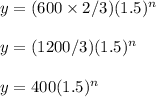
For culture B,

`y=(10* 1/2)(2)^n\\\\y=5(2)^n`

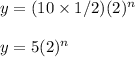
To find which is greater at 18 hours, substitute 18 for n in each:

Culture A:

y = 400(1.5)¹⁸ = 591,156.752

Culture B:

y = 5(2)¹⁸ = 1,310,720

Culture B is greater.

Answer 2

It's B

Explanation: