Explanation:

In this method , the second order of polynomial ax² + bx + c is factorised and expressed as the product of two linear factors. Then each linear factor is separately solved to get the required solutions of the equation by applying zero factor property. In zero factor property , if p•q = 0 , then either p = 0 or q = 0 . In other words , if the product of two numbers is 0 , then one or both of the numbers must be 0.
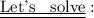
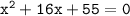
Here , we have to find the two numbers that multiplies to 55 and adds to 16.
⤑
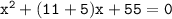
⤑
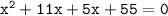
⤑
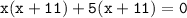
⤑
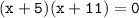
Either :
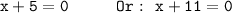



Hope I helped ! ♡
Have a wonderful day / night ! ツ
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁