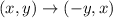Question

Identify the rotation rule on a coordinate plane that verifies that triangle A(2,-1), B(4,1), C(3,3) and triangle A'(1,2), B'(-1,4), C'(-3,3) are congruent when rotated 90°.

Answer 1

Answer:the map notation is (x,y) to (y,-x) at a 90 degree angle

180 degrees map notation is (x,y) to (-x,-y)

360 degrees map notation is (x,y) to (-y,x)

Step-by-step explanation: the answer is they are congruent

Answer 2

Given the coordinates of triangle ABC are A(2,-1), B(4,1), C(3,3) and coordinates of triangle A'B'C' are A'(1,2), B'(-1,4), C'(-3,3).

To find the rotation rule that verifies that the triangle ABC and A'B'C' are congruent.

The rule of rotation of 90 degree counterclockwise is given by:

`(x, y) \rightarrow (-y, x)`

`A(2, -1) \rightarrow (-(-1), 2)=(1, 2) =A'`

`B(4, 1) \rightarrow (-1, 4)=B'`

`C(3, 3) \rightarrow (-3, 3)=C'`

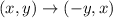
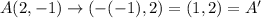
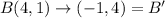
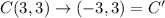
Therefore, the rotation rule that verifies that the triangle ABC and A'B'C' are congruent is
`(x, y) \rightarrow (-y, x)`