Question

What polynomial equation of the least degree has -2,-2,3, and 3 as four of its roots?

Answer 1

f(x) =
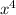`x^(4)` - 2x³ - 11x² + 12x + 36

Explanation:

given that x = a and x = b are the roots of a polynomial then

(x - a) and (x - b) are it's factors and the polynomial is the product of the factors

here x = -2 ( repeated ) and x = 3 (repeated), hence the factors are

(x + 2)² and (x - 3)² → the square denotes a repeated root

f(x) = (x + 2)²(x - 3)² ← expand factors and simplify

= (x² + 4x + 4)(x² - 6x +9)

=
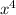`x^(4)` - 2x³ - 11x² + 12x + 36 ← is a possible equation