Question

NEED ANSWER ASAP PLEASE

Solve the turtle and rabbit problem.

In a race between a turtle and a rabbit, the turtle gets a 7-kilometer head start and runs at 2 kilometers per hour. If the rabbit runs at 7 kilometers per hour (with no head start), how long will it take for the rabbit to catch the turtle - that is, when are their distances equal to each other?

Let d = distance traveled by each animal , in kilometers.

Let t = time each animal has been racing, in hours.

1. Write your system of equations.(2 points)

2. Use substitution to solve the system of equations. Show your work.(3 points)

3. Two extra points to give the answer in hours and minutes.

Answer 1

I don't get how it would be a system of equations.

Answer 2

After 1 hour and 24 minutes.

Explanation:

The turtle.

• It gets 7 kilometers head start.
• Its speed is 2 kilometers per hour.

The rabbit.

• It doesn't get any head start.
• Its speed is 7 kilometers per hour.

We know that,
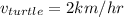`v_(turtle) = 2km/hr` and
`v_(rabbit)= 7km/hr`

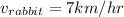
Assuming both have a constant movement, we define each one with

`d=vt`

`d_(rabbit)=v_(rabbit)t` and
`d_(turtle)=v_(turtle)t`, replacing values, we have

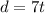`d=7t` which is the distance of the rabbit, and we know the turtle's is +7, so

`d=2t+7`.

Now, we substute the first equation into the second one,

`7t=2t+7\\7t-2t=7\\5t=7\\t=(7)/(5)hr`

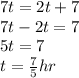
If we divide, we'll have a mixed number

`t=(7)/(5)=1(2)/(5)= 1 \ hr \ 24 \ min`

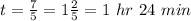
Therefore, the time they will meet is after 1 hour and 24 minutes.