Question

A certain company's main source of income is selling cloth bracelets. The company's annual profit (in thousands of dollars) as a function of the price of a bracelet (in dollars) is modeled by: P(x)=-2x^2+16x-24. What is the maximum profit that the company can earn?

Answer 1

8

Explanation:

Answer 2

8 thousand dollars

Explanation:

The company's annual profit (in thousands of dollars) as a function of the price of a bracelet (in dollars) is modeled by: P(x)=-2x^2+16x-24

To find maximum profit , we need to find out the vertex

x coordinate of vertex formula is -b/2a

`P(x)=-2x^2+16x-24`

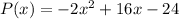
a=-2 and b = 16

`x= (-b)/(2a)= (-16)/(2(-2)) = 4`

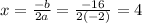
Now we plug in 4 for x and find out P(4)

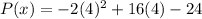`P(x)=-2(4)^2+16(4)-24`= 8

So the maximum profit the company can earn is 8 thousand dollars when price = $4