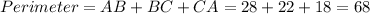Answer:
68 cm
Explanation:
When you have a circle, and an external point
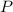 , the two segments
, the two segments
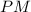 and
and
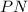 that are tangent to the circle are congruent always. (See Figure 1).
that are tangent to the circle are congruent always. (See Figure 1).
In this case, we can apply the same theorem three times in you figure! (See figure 2)
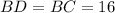
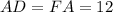

Then, we can find the size of the sides:
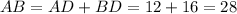
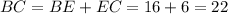
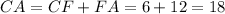
Finally, we can find the perimeter that is the sum of the three sides: