Question

Does each function describe exponential growth or decay?

Drag and drop the equations into the boxes to correctly complete the table.
20 POINTS

Answer 1

Greetings!

Answer:

Growth: Equation 2

Decay: Equation 1,3,4,5

Explanation:

Anything that has a total value of below 1 before the power experiences exponential decay, as you are decreasing.

For the first one:

y = 100(0.5)
`^t` , this is experiencing decay as multiplying the 0.5 by an increasing power will decrease the amount the 100 is multiplied with.

Second one:

y = 0.1(1.25)
`^t` , this is displaying exponential growth because the value inside the brackets is higher than one, and whatever number this is multiplied with in the power it will increase.

Third one:

y = ((0.097)
`^0.5`)
`^(2t)` , is showing exponential decay because the amount inside the brackets (0.97) is constantly being multiplied with the 0.5 power, which decreases the number below one.

Fourth one:

This is showing decay because the number inside the brackets is lower than one.

Fifth one:

This is also showing decay because the number inside the brackets are lower than 1.

Hope this helps!

Answer 2

Growth function = 2nd

Decay function = 1st, 3rd, 4th, 5th

Explanation:

The general exponential function is

`y=ab^x`

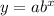
where, a is the initial value and b is growth or decay factor.

If 0<b<1, then it is a decay function and if b>1, then it is a growth function.

In function 1,

`y=100(1-(1)/(2))^t`

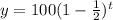
It can be rewritten as

`y=100(0.5)^t`

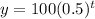
Since b=0.5<1, therefore it is a decay function.

Similarly,

In function 2,

`y=0.1(1.25)^t`

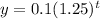
b=1.25>1, therefore it is a growth function.

In function 3,

`y=((1-0.03)^{(1)/(2)})^(2t)=0.97^t`

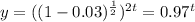
b=0.97<1, therefore it is a decay function.

In function 4,

`y=426(0.98)^t`

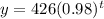
b=0.98<1, therefore it is a decay function.

In function 5,

`y=2050((1)/(2))^t=2050(0.5)^t`

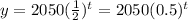
b=0.5<1, therefore it is a decay function.

Therefore, only 2nd function is growth function and all other functions are decay function.