Answer:
1.27 sec
Explanation:
From the given information:
For the ball, Moment of inertia
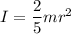
When the height h of the ball is:
h = 4.0 sin 45.4°
and the initial potential energy = mgh
⇒ mg(4.0 sin 45.4°)
According to the conservation of energy.

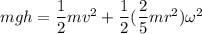
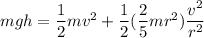
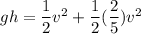
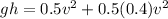
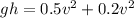
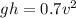
∴
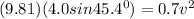
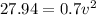
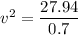

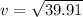
v = 6.32 m/s
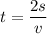
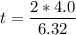
t = 1.27 sec