Question

The table shows a linear function.
which equation represents the function?

Answer 1

Option C is correct.

The equation
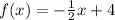`f(x)= -(1)/(2)x +4` represents the function.

Explanation:

Using slope intercept form to find the equation of line :

For any two points
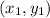`(x_1, y_1)` and
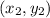`(x_2, y_2)` the equation of line is given by:

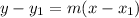`y -y _1 = m(x-x_1)` ......[1] ;where m is the slope given by:

`m = (y_2-y_1)/(x_2-x_1)`

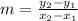
Consider any two points from table :

let (4, 2) and (0, 4) be any two points.

calculate slope:

`m = (y_2-y_1)/(x_2-x_1)= (4-2)/(0-4)`

`m = (2)/(-4) = -(1)/(2)`

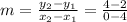
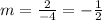
Now, substitute in equation [1] we have:

`y - 2 = -(1)/(2) (x-4)`

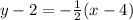
Distributive property i.e,
`a\cdot (b+c) = a\cdot b + a\cdot c`

`y -2 = -(1)/(2)x +2`

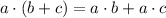
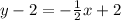
Add both sides 2 we get;

`y -2+2 = -(1)/(2)x+2+2`

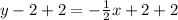
Simplify:

`y = -(1)/(2)x+4`

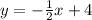
Since, y= f(x)

`f(x)= -(1)/(2)x +4`

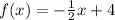
therefore, the equation
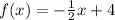`f(x)= -(1)/(2)x +4` represents the function.