Question

A hotel wants to put a fence around a circular spa. The radius of the spa is feet. If the fence is built along the immediate edge of the spa, what is the perimeter of the fence? (Recall that the perimeter of a circle is , where r is the radius of the circle.)

Answer 1

For this case we must find the perimeter of the fence, in a circular way, knowing that the perimeter of a circle is given by:

`P = 2 \pi*r`

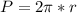
Where "r" represents the radius of the circle, in this case
`r = \frac {5} {\sqrt {2} -1}`

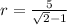
Substituting in the perimeter equation we have:

`P = 2 \pi * \frac {5} {\sqrt {2} -1}`

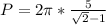
Rationalizing we have:

`P = \frac {2 \pi * 5 (\sqrt {2} +1)} {(\sqrt {2} -1) * (\sqrt {2} +1)}\\P = \frac {2 \pi*5 \sqrt {2} +2 \pi*5} {2-1}\\P = 10 \pi \sqrt {2} +10 \pi`

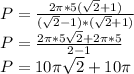
Taking out common factor
`\pi`:

`P = (10 \sqrt {2} +10) \pi`

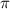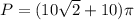
Answer:

`P = (10 \sqrt {2} +10) \pi\ feet`

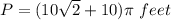
Option C