Answer:
1-D)40
2-D
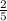
3-B)

4 There are 120 permutations.
5 There are 165 combinations.
6 Sample space is {HH,HT,TH,TT}
Explanation:
Number 1
Step 1
The fundamental counting theorem states that for process that can be carried out in k steps where the fist step can be done in
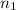 ways, step 2 can be done in
ways, step 2 can be done in
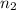 number of ways and the
number of ways and the
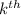 can be done in
can be done in
 number of ways, the number of ways to complete this task is
number of ways, the number of ways to complete this task is
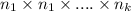 ways.
ways.
Step 2
We now realize that this process can be carried out in 2 steps , there are 8 ways to complete the first step and 5 ways to complete the second step. The number of ways to carry out this calculation is shown below,
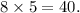 The correct answer is D.
The correct answer is D.
Number 2
Step 1
in this step we calculate the number total number of cans in the ice chest. Since there are 30 red cans and 20 green cans, there is a total of 50 cans.
Step 2
In this step we find the probability of grabbing a green can by dividing the total number of green cans by the total number of cans. The calculation for the probability is shown below,
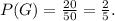
The correct answer is D.
Number 3
Step 1
The first step is to realize that there is a
 chance of getting a head when flipping a coin. When a die is rolled the sample space is {1,2,3,4,5,6}. From this we can tell that there are 3 out of 6 ways to get an even number from this sample space. The probability for an even number is
chance of getting a head when flipping a coin. When a die is rolled the sample space is {1,2,3,4,5,6}. From this we can tell that there are 3 out of 6 ways to get an even number from this sample space. The probability for an even number is

Step 2
The second step in this process is to realize that these two events are independent hence we multiply the individual probabilities of the different outcomes to get the odds of a head and an even number. This calculation is shown below,
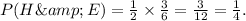
The correct answer is D
Number 4
Step 1
The first step is to realize that the only unique letters in INNOVATIVE are {I,N,O,V,A,T,E}, i.e there are only seven unique permutations of these letters.
Step 2
The second step is to calculate the number of 4 permutations of 7 objects.
This is calculated as shown below,

There are 210 unique permutations of these letters.
Number 5
Step 1
Realize that the number of r combinations of n objects is ,
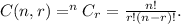
Step 2
We realize that in this problem we have to make 3 combinations of 11 objects. The calculation to determine the number of combination sis shown below,
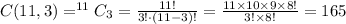
Number 6
Step 1
We list the outcomes where we first get a head. These outcomes are {HH,HT}. Next we list the outcomes in which we get a tail first. These outcomes are {TH,TT }
Step 2
In this step we combine all the outcomes step 1. The combined list of outcomes is {HH,HT, TH, TT}