Question

⦁ The population of the Tallahassee metropolitan area was 382,627 at the end of 2017 with a growth rate of 2.78%. Using the exponential growth formula, sketch the graph that represents the situation. Label the axes, y-intercept and the point that represents the projected population in 2025.

Answer 1

The exponential growth model for the population of the Tallahassee metropolitan area is
`y=382627(1.0278)^t`.

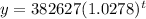Explanation:

The exponential formula is

`y=b(1+r)^t`

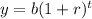
Where b is initial population, r is growth rate, (1+r) is growth factor and t is time (in years) after the initial year.

The population of the Tallahassee metropolitan area was 382,627 at the end of 2017. The growth rate is 2.78%.

Here the initial year is 2017 and rate is 0.0278

`y=382627(1+0.0278)^t`

`y=382627(1.0278)^t`

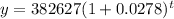
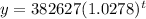
Graph of the equation is shown below. The x-axis represents the number of years after 2017 and y-axis represents the total population.

Difference between 2025 and 2017 is 8 years. Put t=8

`y=382627(1.0278)^8`

`y=382627(1.0278)^8`

`y=476479.828188\approx 476479`

Therefore the projected population in 2025 is 476479.