Question

A silver cube with an edge length of 2.28 cm and a gold cube with an edge length of 2.75 cm are both heated to 82.8 ∘C and placed in 111.5 mL of water at 20.2 ∘C . What is the final temperature of the water when thermal equilibrium is reached?

Answer 1

Given :

length of silver cube = 2.28 cm

length of gold cube = 2.75 cm

Initial temperature = 82.8°C

Volume of silver cube is

Volume
`$=(\text{edge length})^3$`

=
`$(2.28)^3$`

`$= 11.8 \ cm^3$`

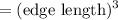
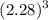
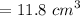
mass of silver cube

Mass,
`$m_s = \text{density} * \text{volume} $`

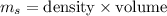
= 10.5 x 11.8

= 123.9 g

Similarly, the volume of gold cube is

Volume
`$=(\text{edge length})^3$`

=
`$(2.75)^3$`

`$= 20.79 \ cm^3$`

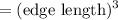
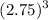
mass of gold cube

Mass,
`$m_g = \text{density} * \text{volume}$`

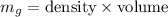
= 19.3 x 20.79

= 401.247 g

Now

heat lost by silver and gold cube = heat gained by water

∴
`$m_g .c_g \Delta T + m_s .c_s \Delta T = m_w.c_w \Delta T$`

`$m_g .c_g (82.8- T) + m_s .c_s (82.8- T) = m_w.c_w (T - 20.2)$`

`$401.247 * 0.1264 (82.8- T) + 123.9 * 0.2386 (82.8- T) = 111.5 * 4.184 (T - 20.2)$`

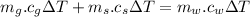
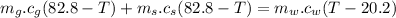
Now solving the equation

`$50.71 (82.8- T) + 29.56 (82.8- T) = 466.51 (T - 20.2)$`

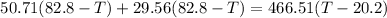
Final temperature, T = 31.27°C