Question

Arbitron Media Research Inc. conducted a study of the iPod listening habits of men and women. One facet of the study involved the mean listening time. It was discovered that the mean listening time for a sample of 10 men was 32 minutes per day. The standard deviation was 19 minutes per day. The mean listening time for a sample of 16 women was also 32 minutes, but the standard deviation of the sample was 9 minutes. At the 0.02 significance level, can we conclude that there is a difference in the variation in the listening times for men and women?

Answer 1

The null and alternative hypotheses are:

`H_(0):\sigma_(men) = \sigma_(women)`

`H_(a):\sigma_(men) \\eq \sigma_(women)`

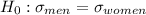
Under the null hypothesis, the test statistic is:

`F=(\sigma^(2)_(men))/(\sigma^(2)_(women))`

`=(19^(2))/(9^(2))`

`=(361)/(81)`

`=4.46`

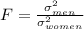
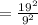
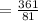
Therefore, the test-statistic is
`F=4.46`

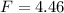
Now the F critical value at 0.02 significance level for df1 = 10- 1 =9 and df2 = 16 - 1 =15 is:

`F_(critical) = 3.303`

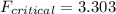
Since F statistic is greater than the F critical value, we therefore, reject the null hypothesis and conclude that there is sufficient evidence to support the claim that there is a difference in the variation in the listening times for men and women.