Question

Find the most general antiderivative of the function. (Check your answer by differentiation. Use C for the constant of the antiderivative. Remember to use absolute values where appropriate.) f(x) = x5 - x3 + 8x - x4

Answer 1

`(x^6)/(6)- (x^5)/(5)- (x^4)/(4) +4x^2+C`

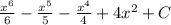
Explanation:

Step 1

The first step is to rearrange the function so that powers of x are in descending form as show below,

`f(x)=x^5-x^3+8x-x^4=x^5-x^4-x^3+8x`

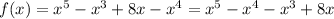
Step 2

The second step is to realize that the anti derivative is the indefinite integral of the function . We compute the integral and then add the constant C in the end. We will use the result that

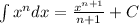`\int x^ndx=(x^(n+1))/(n+1) +C` on every term of the fraction.

This calculation is shown below,

`\int f(x)dx=\int \bigl( x^5-x^4-x^3+8x\bigr)dx\\\int f(x)dx=\bigl((x^(5+1))/(5+1) -(x^(4+1))/(4+1)- (x^(3+1))/(3+1)+(8x^(1+1))/((1+1))+C  \bigr)\\\int f(x)dx= (x^6)/(6)- (x^5)/(5)- (x^4)/(4) +4x^2+C`

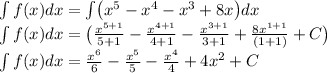
Step 3

The third step is to verify using differentiation that the indefinite integral is correct. We will do this by differentiating every term of the integral with respect to x as shown below

`(d)/(dx) \bigl[(x^6)/(6) -(x^5)/(5)- (x^4)/(4) +4x^2+c\bigr]=6\cdot(x^(6-1))/(6)-5\cdot(x^(5-1))/(5)-4\cdot(x^(4-1))/(4)+2\cdot 4x^(2-1)+0=x^5-x^4-x^3+8x`

This shows that the integral is indeed correct.