Answer:
A:
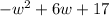
B:

Explanation:
We have been given that the area of Jocelyn's village is represented by the polynomial
 . The area of Lorlesha's village is represented by the polynomial
. The area of Lorlesha's village is represented by the polynomial
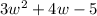 , where w represents the width, in meters of their Town hall.
, where w represents the width, in meters of their Town hall.
A: To find the expression that will represent the additional area of Jocelyn's village, we will subtract the total area of Lorlesha's village from the total area of Jocelyn's village.
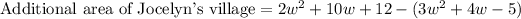
Let us distribute negative sign to simplify our expression.
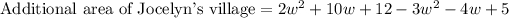
Upon combining like terms we will get,

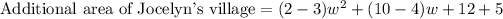

Therefore, the expression that represents the additional area Jocelyn's village is
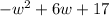 .
.
B: To find the expression that represents the combined total area of their villages we will add areas of Jocelyn's and Larlesha's village.

Upon combining like terms we will get,
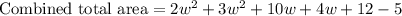
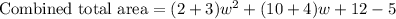
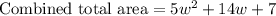
Therefore the expression represents the combined total area of their villages is
 .
.