Question

For the triangles to be congruent by HL, what must be the value of x?

Answer 1

x must be 4 3

3 times 4 is 12 plus 3 is 15

and 15 is what HL is on the other triangle

Answer 2

Answer: The required value of x is 4.

Step-by-step explanation: We are given that the triangles ABC and IGH congruent by HL, where

AB = 9 units, BC = 12 units, AC = 15 units, IH = 3x + 3 and IG = 2x + 1.

We are to find the value of x.

Since the triangles ABC and IGH are congruent by HL rule, so we have

`AB=IG,\\\\AC=IH.`

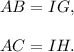
That is,

`AC=IH\\\\\Rightarrow 15=3x+3\\\\\Rightarrow 3x=15-3\\\\\Rightarrow 3x=12\\\\\Rightarrow x=(12)/(3)\\\\\Rightarrow x=4.`

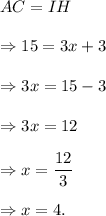
Thus, the required value of x is 4.