Question

What is an equation of a parabola with the given vertex and focus? vertex: (5,4) ; focus: (8,4)

Answer 1

(y - 4)² = 12(x - 5)

Explanation:

the vertex and focus lie on the principal axis y = 4

The focus is inside the parabola to the right of the vertex

This is therefore a horizontally opening parabola

with equation

(y - k)² = 4p(x - h)

where (h, k) are the coordinates of the vertex and p is the distance from the vertex to the focus/ directrix

here p = 8 - 5 = 3

The directrix is vertical and to the left of the vertex with equation x = 2

From any point (x, y) on the parabola the focus and directrix are equidistant

using the distance formula, then

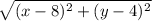`√((x-8)^2+(y-4)^2)` = | x - 2 |

squaring both sides

(x - 8)² + (y - 4)² = (x - 2)²

(y - 4)² = (x - 2)² - (x - 8)² = x² - 4x + 4 - x² + 16x - 64 = 12x - 60

(y - 4)² = 12(x - 5) ← equation of parabola