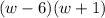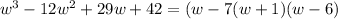Answer:
(w-7(w+1)(w-6)
Explanation:
given that one of the factors is (w − 7)
Divide the given expression by w-7
Use long division
w^2 -5w - 6
-------------------------------------
w-7 w^3 − 12w^2 + 29w + 42
(-)w^3 - 7w^2
-------------------------------------------
-5w^2 + 29w
(-)-5w^2 + 35 w
----------------------------------------------------
-6w + 42
(-) -6w + 42
--------------------------------------------------
0
--------------------------------------------------
Now we factor the quotient w^2 -5w - 6

We need two factors whose sum is -5 and product is -6
-6 and 1 gives us sum -5 and product -6