Question

`\underline{ \underline{ \text{Question}}} :`

In the adjoining figure , ABC is an isosceles triangle. BO and CO are the bisectors of
`\angle` ABC and
`\angle` ACB respectively. Prove that BOC is an isosceles triangle.

~Thanks in advance !

Answer 1

GiveN :-

• In the given figure , ABC is an isosceles triangle.
• BO and CO are the bisectors of
  `\angle` ABC and
  `\angle` ACB respectively.

To ProvE :-

• ∆ BOC is isosceles.

ProoF :-

Here it's given that ∆ABC is a isosceles triangle. We know that in a isosceles triangle opposite angles are equal. And the angles opposite to equal sides are also equal.

Hence here ,

• AB = AC
• ∠ ABC = ∠ACB .

Figure :-

`\setlength{\unitlength}{1 cm}\begin{picture}(12,12)\put(0,0){\line(1,0){4}}\put(4,0){\line(-1,2){2}}\put(0,0.001){\line(1,2){2}}\put(0,0.01){\line(1,1){2}}\put(3.99,0){\line(-1,1){2}}\put(0,-0.3){$\bf B $}\put(4,-0.3){$\bf C$}\put(2,4.2){$\bf A$}</p><p>\put(1.8,2.2){$\bf o$}\end{picture}`

If LaTeX doesn't work on app kindly see the attachment .

Here we will use a theorem which is ,

`\large\underline{\underline{\textsf{\textbf{\red{\blue{$\leadsto$} Theorem :- }}}}}`

• Sides opposite to equal angles are equal.

Hence here,

`\tt:\implies \angle ABC =\angle ACB \\\\\tt:\implies (1)/(2)* \angle ABC = (1)/(2)* \angle ACB \\\\\tt:\implies \boxed{\bf \blue{\angle OBC = \angle OCB} }`

Now in ∆OBC , we can see that ∠OBC = ∠OCB. (just proved ) . Hence we can say that sides OB and OC are equal. Since the sides opposite to equal angles are equal. Therefore in ∆OBC , two sides are equal.

Therefore ∆ OBC is an isosceles triangle.

Hence Proved !

Answer 2

See Below.

Explanation:

We are given the isosceles triangle ΔABC. By the definition of isosceles triangles, this means that ∠ABC = ∠ACB.

Segments BO and CO bisects ∠ABC and ∠ACB.

And we want to prove that ΔBOC is an isosceles triangle.

Since BO and CO are the angle bisectors of ∠ABC and ∠ACB, respectively, it means that ∠ABO = ∠CBO and ∠ACO = ∠BCO.

And since ∠ABC = ∠ACB, this implies that:

∠ABO = ∠CBO =∠ACO = ∠BCO.

This is shown in the figure as each angle having only one tick mark, meaning that they are congruent.

So, we know that:

`\angle ABC=\angle ACB`

∠ABC is the sum of the angles ∠ABO and ∠CBO. Likewise, ∠ACB is the sum of the angles ∠ACO and ∠BCO. Hence:

`\angle ABO+\angle CBO =\angle ACO+\angle BCO`

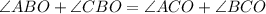
Since ∠ABO =∠ACO, by substitution:

`\angle ABO+\angle CBO =\angle ABO+\angle BCO`

Subtracting ∠ABO from both sides produces:

`\angle CBO=\angle BCO`

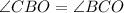
So, we've proven that the two angles are congruent, thereby proving that ΔBOC is indeed an isosceles triangle.