Question

What conclusions can be made using the following information (first and second derivatives):

1. f’(3) = 0 , f’’(3) = -2

2. f’(-2) = 0 , f’’(-2) = 2

3. f’(4) = 0 , f’’(4) = 0

Answer 1

Explanation:

1. There is a local maximum at 3 sice the derivative is null and f"(3)≤0
2. There is a local minimum since f'(-2)=0 and f"(-2)≤0
3. 4 here could be inflection point since f"(4)=0

Answer 2

The Second Derivative Test asserts that

• f'(c) = 0 and f''(c) > 0 implies that f has a local minimum at c
• f'(c) = 0 and f''(c) < 0 implies that f has a local maximum at c.

Intuitively, f''(c) > 0 means a smiley face so any critical number of f where f'(c) = 0 should result in a local minimum, the local bottom extreme of the happy face. f''(c) < 0 means a frowning face so any critical number of f where f'(c) = 0 should result in a local maximum, the local top extreme of the happy face

It is inconclusive when f''(c) = 0 or f''(c) does not exist. (For example, consider
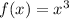`f(x) = x^3`. It has no local maxima or minima, yet
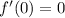`f'(0) = 0` and
`f''(0) = 0`.)

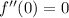Therefore,

1. From f’(3) = 0 and f’’(3) = -2, we can conclude that f has a local maximum at 3.
2. From f’(-2) = 0 and f’’(-2) = 2, we can conclude that f has a local minimum at -2.
3. From f'(4) = 0 and f''(4) = 0, we cannot conclude anything from just those two pieces alone. We cannot determine if f has a local maximum or minimum at 4, nor can we say anything about inflection points since we do not know if f'' changes sign at x = 4.