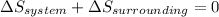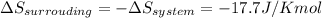Question

What is the entropy change of the surroundings

when 10.8 g of acetone (CH3COCH3)
condenses at its normal boiling of 56.2◦C?

Answer 1

Answer: The entropy change of the surroundings will be -17.7 J/K mol.

Explanation: The enthalpy of vapourization for 1 mole of acetone is 31.3 kJ/mol

Amount of Acetone given = 10.8 g

Number of moles is calculated by using the formula:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

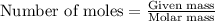
Molar mass of acetone = 58 g/mol

Number of moles =
`(10.8)/(58)=0.1862moles`

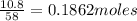
If 1 mole of acetone has 32.3 kJ/mol of enthalpy, then

0.1862 moles will have =
`(32.3)/(1)* 0.1862=5.828kJ/mol`

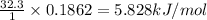
To calculate the entropy change for the system, we use the formula:

`\Delta S_(sys)=\frac{\Delta H_(vap)}{T(\text{ in K)}}`

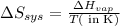
Temperature = 56.2°C = (273 + 56.2)K = 329.2K

Putting values in above equation, we get

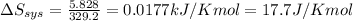`\Delta S_(sys)=(5.828)/(329.2)=0.0177kJ/Kmol=17.7J/Kmol` (Conversion Factor: 1 kJ = 1000J)

At Boiling point, the liquid phase and gaseous phase of acetone are in equilibrium. Hence,

`\Delta S_(system)+\Delta S_(surrounding)=0`

`\Delta S_(surrouding)=-\Delta S_(system)=-17.7J/Kmol`