Question

In parallelogram ABCD, diagonals AC and BD intersect at point E, BE =2x^2-3x, and DE=x^2+10. What is BD? Enter your answer in the box

Answer 1

70

Explanation:

In parallelogram ABCD, diagonals AC and BD intersect at point E

E is the midpoint of BD

So BE = DE

Given: BE =2x^2-3x, and DE=x^2+10

BE = DE

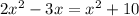`2x^2-3x = x^2+10` (solve for x)

Subtract x^2 and 10 on both sides

`2x^2-3x- x^2-10=0`

`x^2-3x-10=0`

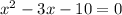
Factor x^2-3x-10

(x-5)(x+2) = 0

x-5 =0 so x=5

x+2=0 so x=-2

Length x cannot be negative so we ignore x=-2

Lets plug in 5 for x and find out BE and DE

BE =
`2x^2-3x= 2(5)^2-3(5)= 50-15= 35`

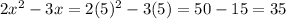
DE =
`x^2+10= (5)^2+10=35`

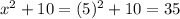
BD = BE + DE= 35+35 = 70

So BD = 70