Question

If $-2 < x \le 3,$ then find all possible values of $5x + 1.$ Give your answer in interval notation PLEASE ANSWER THUS PLEASE

Answer 1

(-9,16]

Explanation:

It is given that

`-2 < x \le 3`

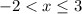
We need to find the possible values of
`5x+1`.

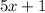Multiply all sides by 5 in the above inequality.

`-2\cdot 5 < x\cdot 5 \le 3\cdot 5`

`-10< 5x\le 15`

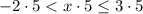
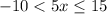
Add 1 on each side.

`-10+1< 5x+1\le 15+1`

`-9< 5x+1\le 16`

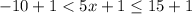
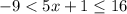
It is clear that the possible values are lie between -9 and 16 (included).

`5x+1\in (-9,16]`

Close bracket represents that 16 is included in the solution set.

Therefore, the required interval is (-9,16].

Answer 2

`(-9,16]`

Explanation:

we know that

The domain of x is equal to the interval-------->
`(-2,3]`

`-2< x \leq 3`

All real numbers greater than
`-2` and less than or equal to
`3`

Let

`y=5x+1`

For
`x=3`

`y=5x+1\\y=5(3)+1=16`

For
`x>-2`

`y >5(-2)+1\\y > -9`

so

The range of the function is the interval-------->
`(-9,16]`