Question

What is the equation of this line in standard form? (Please explain)

A: 6x - 7y = 11
B: 7x - 6y = 11
C: 6x - 5y = -13
D: 6x - 7y = -11

(BTW the point near the bottom of the grid is (-3, -1) in case you can't see it very well in the picture.)

Answer 1

`\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{-1})\qquad (\stackrel{x_2}{(1)/(2)}~,~\stackrel{y_2}{2}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{2-(-1)}{(1)/(2)-(-3)}\implies \cfrac{2+1}{(1)/(2)+3} \\\\\\ \cfrac{3}{~~(7)/(2)~~}\implies \cfrac{3}{1}\cdot \cfrac{2}{7}\implies \cfrac{6}{7}`

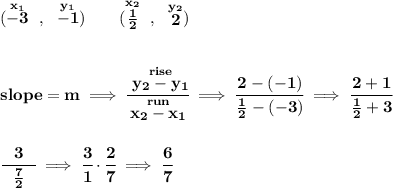
`\bf \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-(-1)=\cfrac{6}{7}[x-(-3)] \\\\\\ y+1=\cfrac{6}{7}(x+3)\implies y+1=\cfrac{6}{7}x+\cfrac{18}{7}\implies y=\cfrac{6}{7}x+\cfrac{18}{7}-1 \\\\\\ y=\cfrac{6}{7}x+\cfrac{11}{7}`

now, let's bear in mind that

standard form for a linear equation means

• all coefficients must be integers, no fractions

• only the constant on the right-hand-side

• all variables on the left-hand-side, sorted

• "x" must not have a negative coefficient

so, let's multiply both sides by the LCD of all fractions, in this case that'd be 7, to do away with the denominators.

`\bf \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{7}}{7(y)=7\left( \cfrac{6}{7}x+\cfrac{11}{7} \right)}\implies 7y=6x+11\implies -6x+7y=11 \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill 6x-7y=-11~\hfill`