Question

Y=(x-3)^2-4

vertex?
x intercepts?
y intercepts?
axis of symmetry?
minimum or maximum?

Answer 1

Steps:

• Vertex Form: y = a(x - h)² + k with (h,k) as the vertex

So firstly, let's start with the vertex. Since this is in vertex form, we can find the vertex easily. Since 3 is in the h variable and -4 is in the k variable, the vertex is (3,-4).

Next, the axis of symmetry. Remember that the vertex's x-coordinate and the axis of symmetry are the same. In this case, since the vertex's x-coordinate is 3, this means that the axis of symmetry is x = 3.

Next, whether the vertex is a minimum or a maximum. To determine whether it's a minimum or a maximum, we look towards the a variable of the vertex form. If a is negative, then the parabola opens down and the vertex is a maximum. However, if a is positive, then the parabola opens up and the vertex is a minimum. In this case, a = 1 and since 1 is positive, this makes the vertex a minimum.

Next, to find the y-intercept plug 0 into the x-variable and solve:

`y=(0-3)^2-4\\y=(-3)^2-4\\y=9-4\\y=5`

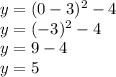
The y-intercept is (0,5).

Next, to find the x-intercepts plug 0 into the y-variable to solve. Since it's a bit less straightforward than finding the y-intercept, I will walk through the steps:

`0=(x-3)^2-4`

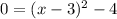
Firstly, add 4 to both sides:

`4=(x-3)^2`

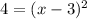
Next, square root both sides:

`\pm\ 2=x-3`

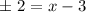
Next, add 3 to both sides:

`3\pm2=x`

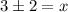
Lastly, solve the left side twice: once with the plus sign, once with the minus sign:

`3+2=x\\5=x\\\\3-2=x\\1=x`

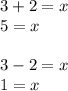
Your x-intercepts are (5,0) and (1,0).

Answers:

In short:

• Vertex: (3,-4)
• x-intercept(s): (5,0) and (1,0)
• y-intercept(s): (0,5)
• Axis of symmetry: x = 3
• Minimum or Maximum? Minimum.