Question

Solve the quadratic equation by factoring: x^2 - 144= 0

x= 12

x= +_12

x= +_16

x = 16

Answer 1

Steps:

• Difference of Squares rule:
  `x^2-y^2=(x+y)(x-y)`
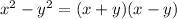
• Zero Product Property: If a × b = 0, then either a or b = 0 or both a and b = 0.

So firstly, apply the difference of squares rule:

`√(x^2)=x\\√(144)=12\\\\x^2-144=(x+12)(x-12)\\\\(x+12)(x-12)=0`

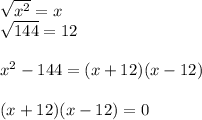
Next, we are going to be applying the Zero Product Property to solve for x as such:

`x+12=0\\x=-12\\\\x-12=0\\x=12`

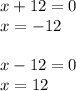
Answer:

In short, x = ± 12 or the 2nd option.

Answer 2

x = +-12

Explanation:

x^2 -144 =0

(x-12) (x+12) =0

using the zero product property

x-12=0 x+12 =0

x=12 x=-12