Question

PLEASE HELP QUICKLY 15 POINTS!!

The table represents a function
X. Y
0. 6
2. 8
4 10
6. 12

complete the statement by selecting from the drop down menu the rate change in the function y = X + 4 is (greater than, less than, equal to) the rate of change in this function represented in the table

Answer 1

The slopes of the two functions are equal.

Explanation:

In this question, we are comparing the rate of change, or "slope," of the two functions.

First, we will find the slope of the given function, y=x+4. This function is in the slope-intercept form, y=mx+b, where m is the slope and b is the y-intercept. In this case, the slope is 1, which is implied.

( y=x+4 is the same as y=1x+4)

The slope for the first equation is 1.

Next, we have to determine the slope of the second function, depicted in the table. This can be done two ways, one is easier, but is very informal.

First method is to count the rise/run, y=rise, x=run.

The difference between the values in the Y side of the table is consistently +2, and the difference for the x values in the table is consistently +2, therefore, the slope is 2/2, which is 1.

The second method is to use the slope formula:

`m = (y_(1) - y_(2))/(x_(1) - x_(2))`

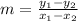
To use this formula, we must pick two points and plug in their coordinates, we will use (0,6) and (2,8).

`m = ((6-8))/((0-2)) = (-2)/(-2) = (1)/(1) = 1`

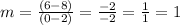
The slope is confirmed to be equal to 1.

Answer 2

equal to

Explanation:

the slope of the function in the table

m = (y2-y1)/(x2-x1)

m = (8-6)/(2-0)

m = 2/2 = 1

the slope is 1

the line given is y = x+4 (y=mx+b)

the slope is 1

the slopes are the same