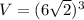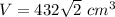Answer:
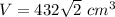
Explanation:
we know that
The volume of a cube is equal to
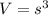
where s is the length side of a cube
The diagonal of the cube in each face is equal to the diameter of the sphere
so
Applying the Pythagoras theorem
Find the length side s of the cube
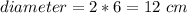
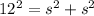
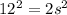
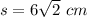
Find the volume of the cube