Question

A rectangular piece of plywood has a diagonal which measures two feet more than the width. The length of the plywood is twice the width. What is the length of the plywood’s diagonal? Round your answer to the nearest tenth.

Answer 1

The length of the plywood's diagonal(to the nearest tenth) is, 3.6 and 1.4

Explanation:

let l be the length and w be the width of the rectangle respectively;

Diagonal(D) of a rectangle is given by:

`D = √(l^2+w^2)` ......[1]

As per the given statement we have;

Diagonal(D) = width + 2

and

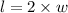`l = 2 * w` = 2w

Now, substitute these in [1] we have;

`√((2w)^2+w^2) = w+5`

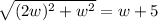
Squaring both the sides we get;

`4w^2+w^2 = (w+2)^2`

`5w^2 = w^2 + 4 + 4w`

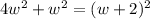
or

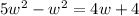`5w^2 -w^2 = 4w + 4` or

`4w^2= 4w + 4`

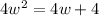
Simplify:

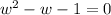`w^2-w-1 =0` ......[2]

The quadratic equation is in the form of
`ax^2+bx+c = 0`

the solution is given by:
`x = (-b \pm√(b^2-4ac))/(2a)`

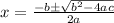
On comparing with [1] we get

a= 1 , b = -1 and c = -1

Then the solution is:

`w= (-(-1) \pm√((-1)^2-4(1)(-1)))/(2(1))`

`w =(1 \pm√(1+4))/(2) = (1 \pm√(5))/(2)`

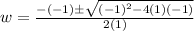
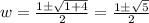
Simplify:

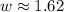`w \approx 1.62` and
`w \approx -0.62`

Then, the diagonal D = w+2

For
`w \approx 1.62`

`D = 1.62 +2 \approx 3.62`

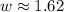
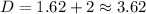
For
`w \approx -0.62`

`D =-0.62 +2 \approx 1.38`

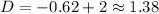
therefore, the length of the plywood's diagonal(to the nearest tenth) is, 3.6 and 1.4