Answer:
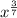
Explanation:
I'd assume your question is to simplify the expression
![\sqrt[7]{x}*\sqrt[7]{x}*\sqrt[7]{x}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/z8ybfpu1two9tolad51cj644yt8or7eqow.png)
There are 2 rules of exponents we are going to use to simplify this expression:
![\sqrt[n]{a} = a^{(1)/(n)}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/jhnkbt037tsxsolodicrgc2hyv6pjcttbp.png) , and
, and
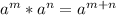
Using RULE 1, we can write the radicals [expression with roots] into exponential form [with a fractional exponent] like this:
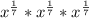
Now, the bases are same,
 , and we have 3 powers. Using RULE 2, we can add the powers like this:
, and we have 3 powers. Using RULE 2, we can add the powers like this:
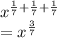
This is the simplified form.