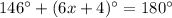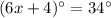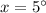Answer: x= 5
Explanation:
Here, An isosceles triangle A B C with vertical base A C and vertex B is in right side of the base. Side A B and B C are labeled with single tick mark.
Therefore, BA= BC ⇒
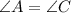
And, All the three angles are labeled. Base angles C A B is labeled as 73 degrees and angle A C B is labeled as left parenthesis 8 y minus 7 right parenthesis degrees.
Therefore,
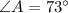 ,
,
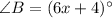 ,
,
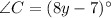
Since, By the property of triangle,
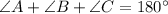
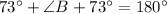 ( because,
( because,
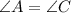 )
)