Question

The number of subscribers to an online magazine is increasing by 34% each year. The function represents the number of subscribers after t years.

f(t) = 13,000(1.34)^t



Which statement is true?

A.
The expression (1.05)6t reveals the approximate rate of increase in the number of subscribers if measured six times a year.
B.
The expression (1.15)3t reveals the approximate rate of increase in the number of subscribers if measured three times a year.
C.
The expression (1.03)4t reveals the approximate rate of increase in the number of subscribers if measured four times a year.
D.
The expression (1.12)2t reveals the approximate rate of increase in the number of subscribers if measured two times a year.

Answer 1

Answer: A. The expression
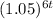`(1.05)^(6t)` reveals the approximate rate of increase in the number of subscribers if measured six times a year.

Explanation:

Here, The number of subscribers to an online magazine is increasing by 34% each year. The function represents the number of subscribers after t years.

`f(t) = 13,000(1.34)^t`

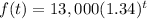
where
`(1.34)^t` represents rate of increase in the number of subscriber.

If rate is measured six times a year

then the number of subscriber,
`f(6t)= 13000(1+0.34/6)^(6t)`

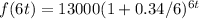
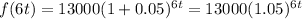`f(6t) = 13000( 1+0.05)^(6t)= 13000(1.05)^(6t)` ( approx)

Thus, when we measure increment in six times a year then the rate rate of increase in the number of subscribers=
`(1.05)^(6t)`

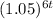
Therefore Option A is correct.

Note: Option B) is incorrect because rate of increase in the number of subscribers if measured three times a year =
`13000(1.11)^(3t)` ( approx)

Option C) is incorrect because rate of increase in the number of subscribers if measured four times a year =
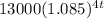`13000(1.085)^(4t)` ( approx)

Option D) is incorrect because rate of increase in the number of subscribers if measured two times a year =
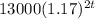`13000(1.17)^(2t)` ( approx)