Question

A research study in the year 2000 found that there were 440 coyotes in a given region. The coyote population is expected to grow at a rate of 17% each year. What is the coyote population in 2006? Round the answer to the nearest whole number. Enter your answer in the box.

Answer 1

1129

Explanation:

The equation for exponential growth is y=A(1+r)^t

A=2000

r (rate)=0.17 (17 as a percent)

t (time)=2006-2000=6

y=440(1+0.17)^6

y=1128.672249

There can't be part of a coyote, therefore y=1129

Answer 2

Find out the what is the coyote population in 2006 .

To prove

As given

A research study in the year 2000 found that there were 440 coyotes in a given region.

The coyote population is expected to grow at a rate of 17% each year.

Thus the increasing exponential function is denoted by.

`y = a(1 +\ r)^(t)`

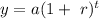
Where a is the intial population .

r is in the decimal form.

t is the time.

Here

a = 440

`r = (17)/(100)`

r = 0.17

t = 6 years (From 2000 to 2006)

Put all the values in the formula

`y = 440*(1 + 0.17)^(6)`

`y = 440* (1.17)^(6)`

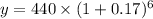
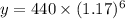
y = 440 × 2.56516

y = 1128.67

Thus

y = 1129 (Rounded to nearest whole number)

Therefore the coyote population in 2006 is 1129.