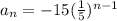Answer:
Option A is correct.
Explanation:
Given:
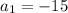 ;
;
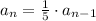
for n = 2
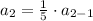 =
=
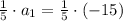
for n =3
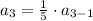 =
=
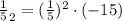
Simlarly , for n =4
 =
=

and so on...
Common ratio(r) states that for a geometric sequence or geometric series, the common ratio is the ratio of a term to the previous term.
we have;

Now; by recursive formula for geometric series:
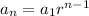
where
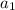 is the first term and r is the common ratio:
is the first term and r is the common ratio:
Substitute the value of
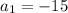 and
and
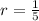
we have;
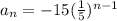
therefore, the explicit rule for the geometric sequence is;