Question

A 2.0-kg object is lifted vertically through 3.00 m by a 150-N force. How much work is done on the object by gravity during this process?

Answer 1

-58.8 J

Step-by-step explanation:

Work done on the object by gravity = Force due to gravity x Displacement

Force due to gravity = weight of the object

= m g

= (2.0 kg) (9.8 m/s²)

= 19.6 N

The force due to gravity acts in downwards direction opposite the direction of the displacement. Thus, the angle between the force and the displacement is 180°.

Work done on the object by gravity

= 19.6 N x 3.00 m x cos 180° = -58.8 J

Answer 2

-58.8 J

Step-by-step explanation:

The work done by a force is given by:

`W=Fdcos \theta`

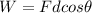
where

F is the magnitude of the force

d is the displacement of the object

`\theta` is the angle between the direction of the force and the displacement.

In this problem, we are asked to find the work done by gravity, so we must calculate the magnitude of the force of gravity first, which is equal to the weight of the object:

`F=mg=(2.0 kg)(9.8 m/s^2)=19.6 N`

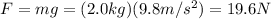
The displacement of the object is d = 3.00 m, while
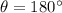`\theta=180^(\circ)`, because the displacement is upward, while the force of gravity is downward; therefore, the work done by gravity is

`W=Fdcos \theta=(19.6 N)(3.00 m)(cos 180^(\circ))=-58.8 J`

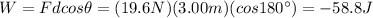
And the work done is negative, because it is done against the motion of the object.