Question

Let f(x)=8(3)x−2+2 .

The graph of f(x) is stretched vertically by a factor of 3 to form the graph of g(x) .

What is the equation of g(x) ?



Enter your answer in the box.

g(x) =

Answer 1

g(x) = 8(3)^x-1 + 6

Explanation:

I took the test, and this was the correct answer! Have a great day!

MERRY CHRISTMAS!!!

Answer 2

g(x) =
`8 (3)^(x-1) + 6`

Explanation:

Given the function:
`f(x) = 8(3)^(x-2) + 2`

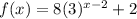
For the parent function f(x) and a constant k >0,

then,

the function given by

g(x) = kf(x) can be sketched by vertically stretching f(x) by a factor of k if k>1

or

if 0 < k < 1 , then it is vertically shrinking f(x) by a factor of k

.

As per the given statement that the graph of f(x) is stretched vertically by a factor of 3 i.e

k = 3 >1

so, by definition

g(x) = 3 f(x) =
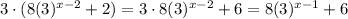`3 \cdot (8(3)^(x-2) + 2) = 3 \cdot 8 (3)^(x-2) +6 = 8 (3)^(x-1) + 6` [Using
`a^n \cdot a^m = a^(n+m)` ]

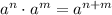Therefore, the equation of g(x) =
`8 (3)^(x-1) + 6`