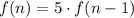Question

The table below represents a geometric sequence.

Determine the recursive function that defines the sequence.

A.
f(1) = 4,
f(n) = 16 · f(n - 1), for n ≥ 2
B.
f(1) = 5,
f(n) = 4 · f(n - 1), for n ≥ 2
C.
f(1) = 4,
f(n) = 5 · f(n - 1), for n ≥ 2
D.
f(1) = 1,
f(n) = 10 · f(n - 1), for n ≥ 2

Answer 1

B. f(1)=4

`f(n)=5\cdot f(n-1)`,
`n\ge2`

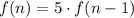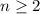
Explanation:

From the table the first term of the geometric sequence is:

`f(1)=4`

We can use the first term and the second term to determine the common rtaio.

The common ratio is

`r=(20)/(4)=5`

Note that, we could have also used the 3rd and second term to find the common ratio.

The recursive formula is given by:

`f(n)=r\cdot f(n-1)`

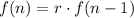
We plug in the common ratio to get:

`f(n)=5\cdot f(n-1)`